NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals

NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Exercise 3.1

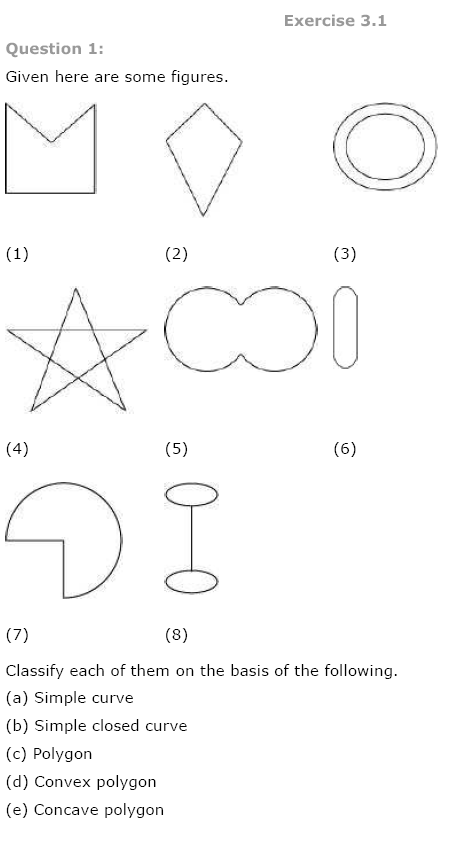
Ex 3.1 Class 8 Maths Question 1.
Given here are some figures.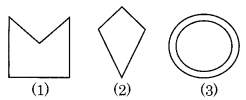

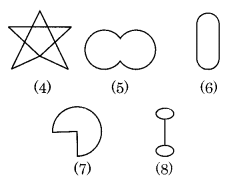
Classify each of the above figure on the basis of the following:
(a) Simple curve
(b) Simple closed curve
(c) Polygon
(d) Convex polygon
(e) Concave polygon
Solution:
(a) Simple curve: (1), (2), (5), (6) and (7)
(b) Simple closed curve: (1), (2), (5), (6) and (7)
(c) Polygon: (1) and (2)
(d) Convex polygon: (2)
(e) Concave polygon: (1)

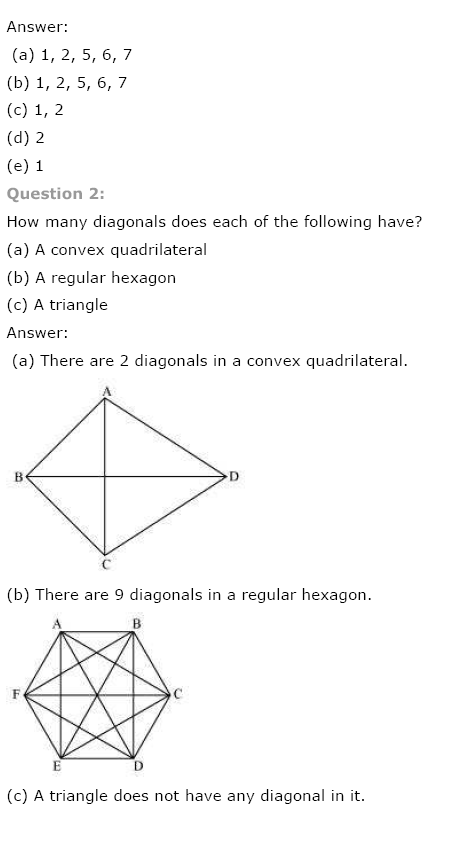
Ex 3.1 Class 8 Maths Question 2.
How many diagonals does each of the following have?
(a) A convex quadrilateral
(b) A regular hexagon
(c) A triangle
Solution:
(a) In Fig. (i) ABCD is a convex quadrilateral which has two diagonals AC and BD.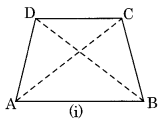

(b) In Fig. (ii) ABCDEF is a regular hexagon which has nine diagonals AE, AD, AC, BF, BE, BD, CF, CE and DF.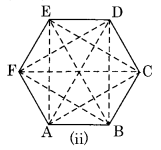

(c) In Fig. (iii) ABC is a triangle which has no diagonal.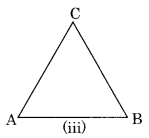

Ex 3.1 Class 8 Maths Question 3.
What is the sum of the measures of the angles of a convex quadrilateral? Will this property hold if the quadrilateral is not convex? (Make a non-convex quadrilateral and verify)
Solution:
In the given figure, we have a quadrilateral ABCD. Join AC diagonal which divides the quadrilateral into two triangles ABC and ADC.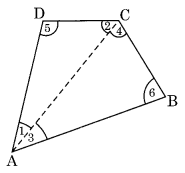

In ∆ABC, ∠3 + ∠4 + ∠6 = 180°…(i) (angle sum property)
In ∆ADC, ∠1 + ∠2 + ∠5 = 180° …(ii) (angle sum property)
Adding, (i) and (ii)
∠1 + ∠3 + ∠2 + ∠4 + ∠5 + ∠6 = 180° + 180°
⇒ ∠A + ∠C + ∠D + ∠B = 360°
Hence, the sum of all the angles of a convex quadrilateral = 360°.
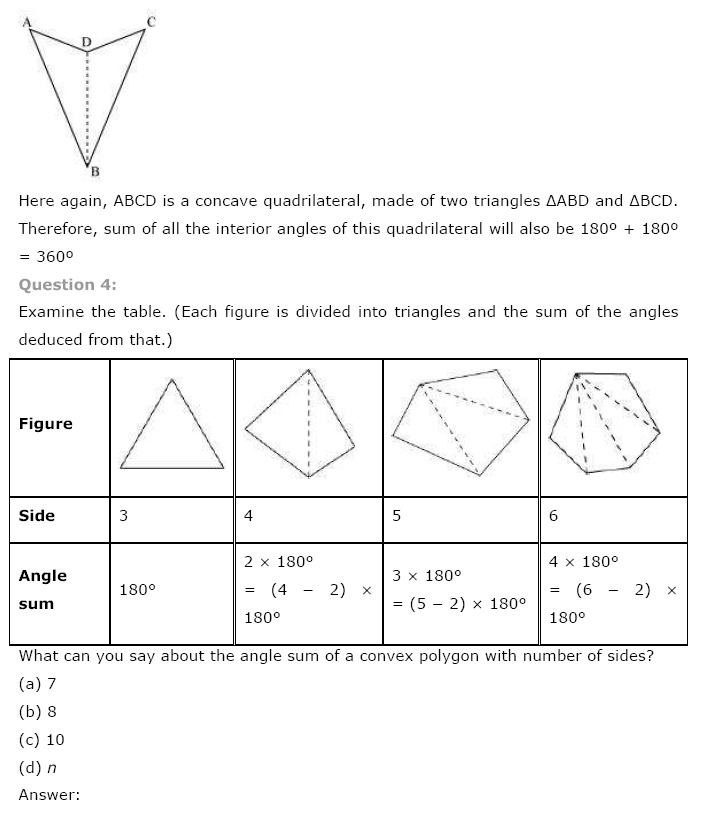
Let us draw a non-convex quadrilateral.
Yes, this property also holds true for a non-convex quadrilateral.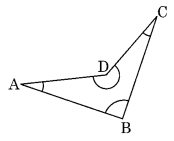

Ex 3.1 Class 8 Maths Question 4.
Examine the table. (Each figure is divided into triangles and the sum of the angles reduced from that).

What can you say about the angle sum of a convex polygon with number of sides?
(a) 7
(b) 8
(c) 10
(d) n
Solution:
From the above table, we conclude that the sum of all the angles of a polygon of side ‘n’
= (n – 2) × 180°
(a) Number of sides = 7
Angles sum = (7 – 2) × 180° = 5 × 180° = 900°
(b) Number of sides = 8
Angle sum = (8 – 2) × 180° = 6 × 180° = 1080°
(c) Number of sides = 10 Angle sum = (10 – 2) × 180° = 8 × 180° = 1440°
(d) Number of sides = n
Angle sum = (n – 2) × 180°

Ex 3.1 Class 8 Maths Question 5.
What is a regular polygon? State the name of a regular polygon of
(i) 3 sides
(ii) 4 sides
(iii) 6 sides
Solution:
A polygon with equal sides and equal angles is called a regular polygon.
(i) Equilateral triangle

(ii) Square

(iii) Regular Hexagon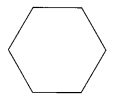

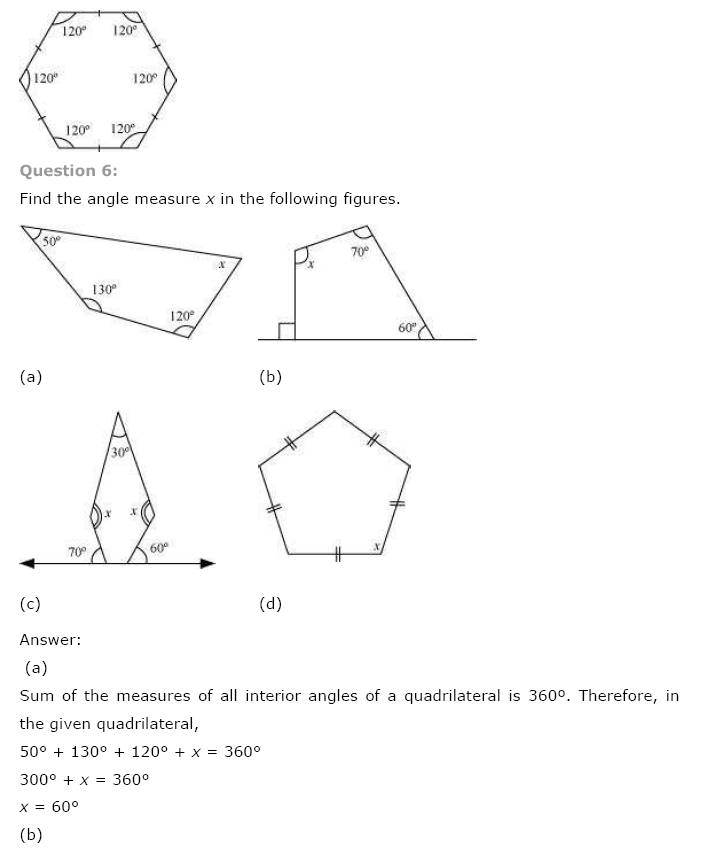
Ex 3.1 Class 8 Maths Question 6.
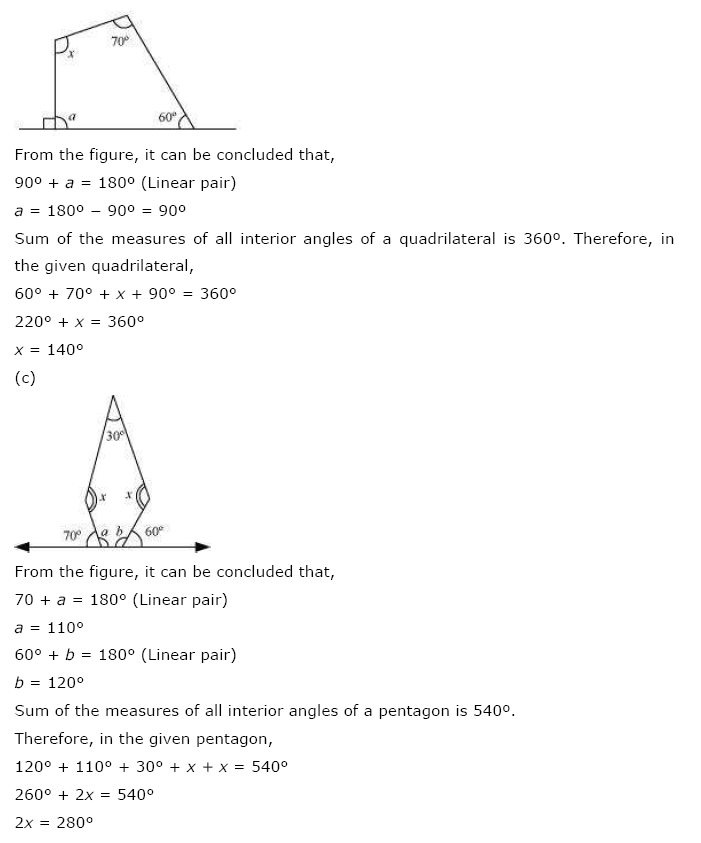
Find the angle measure x in the following figures: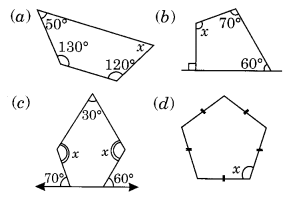

Solution:
(a) Angle sum of a quadrilateral = 360°
⇒ 50° + 130° + 120° + x = 360°
⇒ 300° + x = 360°
⇒ x = 360° – 300° = 60°
(b) Angle sum of a quadrilateral = 360°
⇒ x + 70° + 60° + 90° = 360° [∵ 180° – 90° = 90°]
⇒ x + 220° = 360°
⇒ x = 360° – 220° = 140°
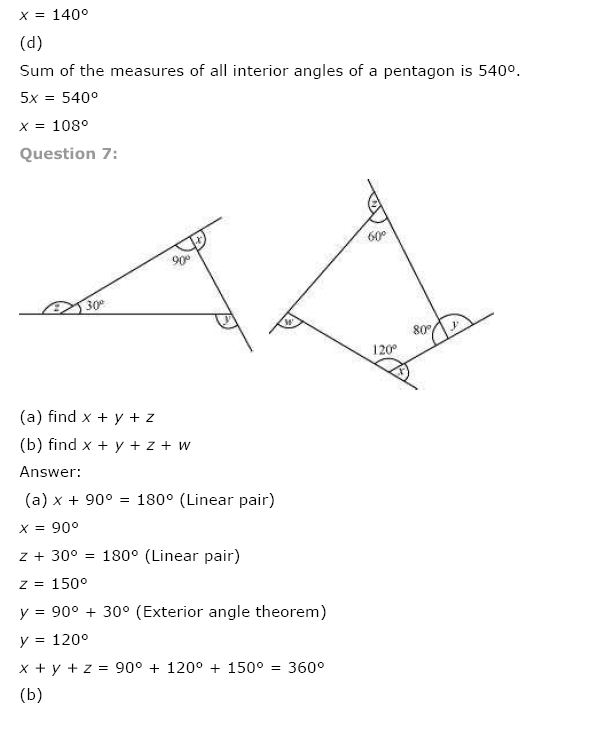
(c) Angle sum of a pentagon = 540°
⇒ 30° + x + 110° + 120° + x = 540° [∵ 180° – 70° = 110°; 180° – 60° = 120°]
⇒ 2x + 260° = 540°
⇒ 2x = 540° – 260°
⇒ 2x = 280°
⇒ x = 140°
(d) Angle sum of a regular pentagon = 540°
⇒ x + x + x + x + x = 540° [All angles of a regular pentagon are equal]
⇒ 5x = 540°
⇒ x = 108°

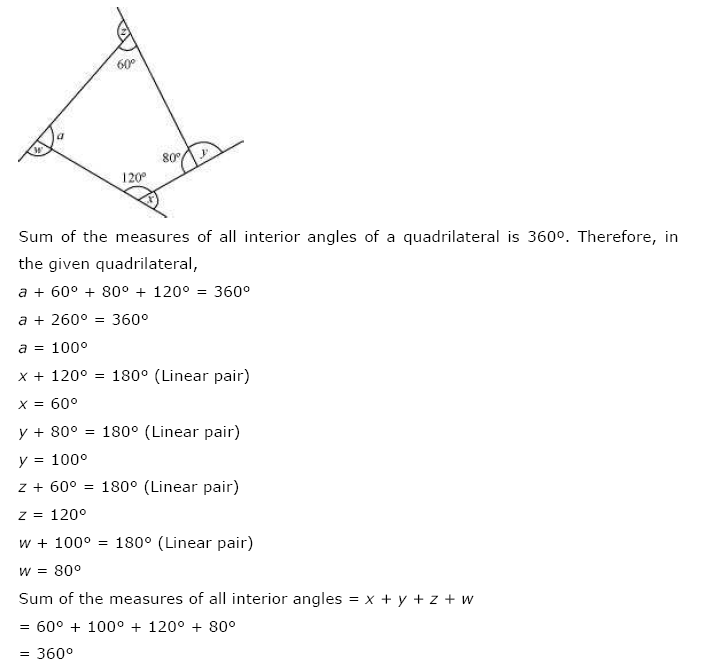
Ex 3.1 Class 8 Maths Question 7.
(a) Find x + y + z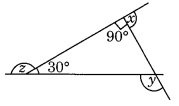

(b) Find x + y + z + w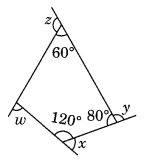

Solution:
(a) ∠a + 30° + 90° = 180° [Angle sum property]
⇒ ∠a + 120° = 180°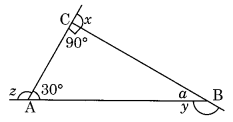

⇒ ∠a = 180° – 120° = 60°
Now, y = 180° – a (Linear pair)
⇒ y = 180° – 60°
⇒ y = 120°
and, z + 30° = 180° [Linear pair]
⇒ z = 180° – 30° = 150°
also, x + 90° = 180° [Linear pair]
⇒ x = 180° – 90° = 90°
Thus x + y + z = 90° + 120° + 150° = 360°
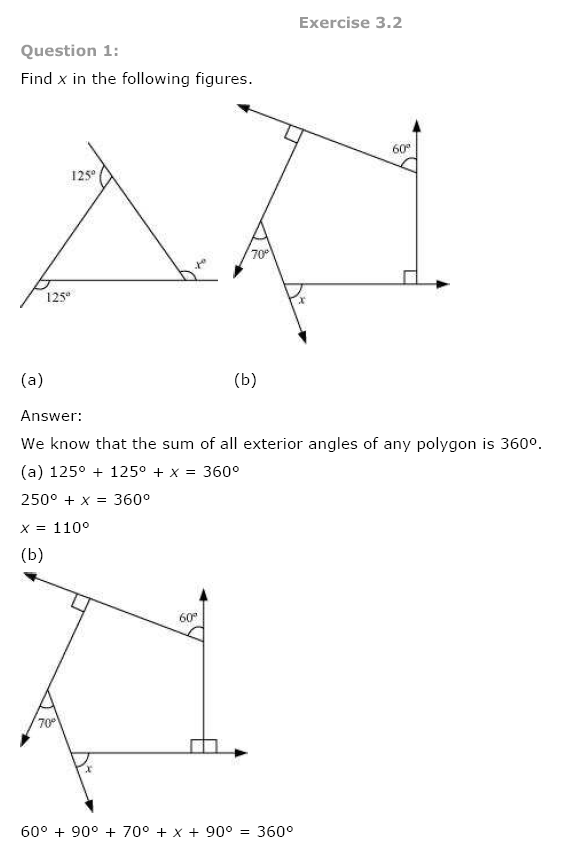
(b) ∠r + 120° + 80° + 60° = 360° [Angle sum property of a quadrilateral]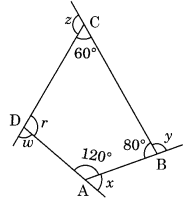

∠r + 260° = 360°
∠r = 360° – 260° = 100°
Now x + 120° = 180° (Linear pair)
x = 180° – 120° = 60°
y + 80° = 180° (Linear pair)
⇒ y = 180° – 80° = 100°
z + 60° = 180° (Linear pair)
⇒ z = 180° – 60° = 120°
w = 180° – ∠r = 180° – 100° = 80° (Linear pair)
x + y + z + w = 60° + 100° + 120° + 80° = 360°.