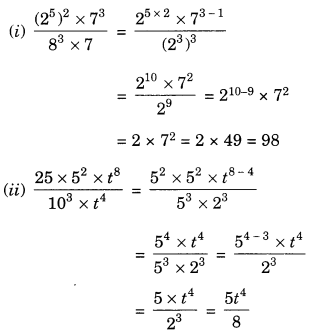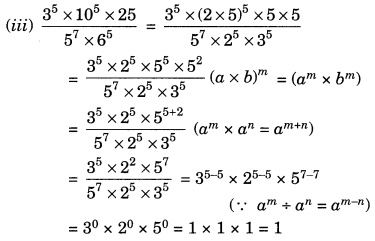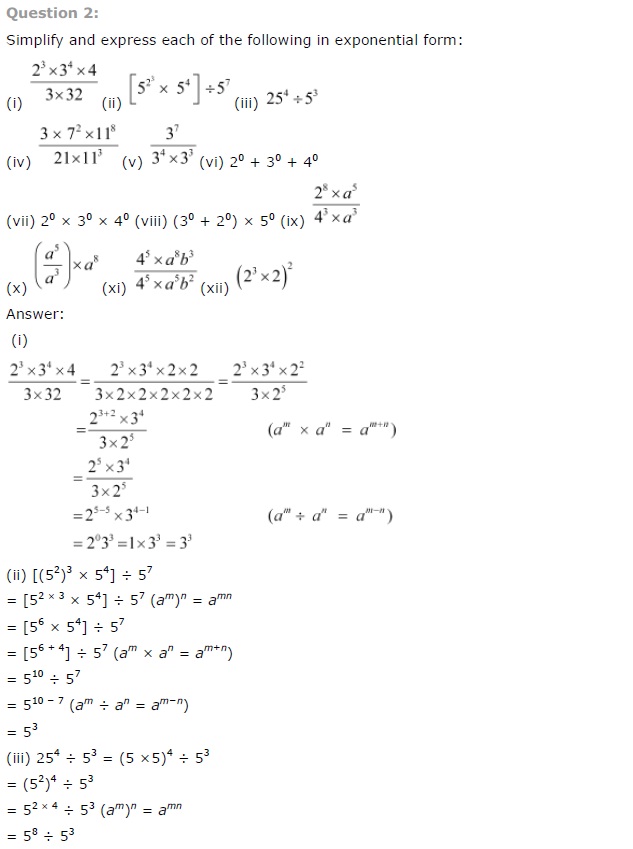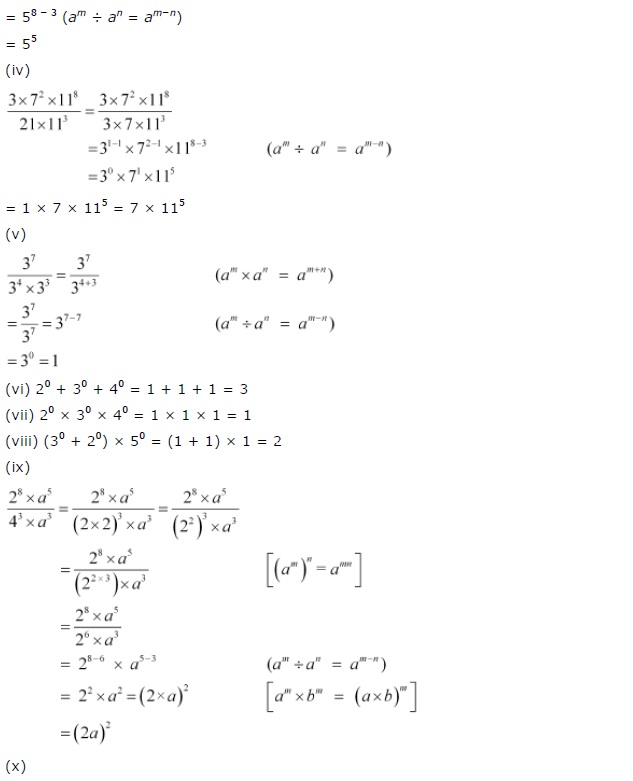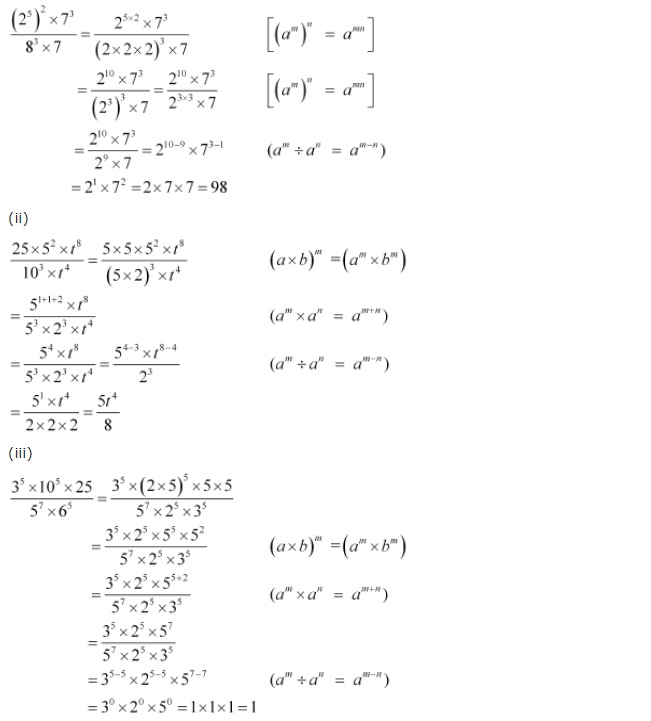NCERT Solutions for Class 7 Maths Chapter 13 Exponents and Powers Ex 13.2
- Class 7 Maths Exponents and Powers Exercise 13.1
- Class 7 Maths Exponents and Powers Exercise 13.2
- Class 7 Maths Exponents and Powers Exercise 13.3
NCERT Solutions for Class 7 Maths Chapter 13 Exponents and Powers Exercise 13.2
Ex 13.2 Class 7 Maths Question 1.
Using laws of e×ponents, simplify and write the answer in e×ponential form:
(i) 32 × 34 × 38
(ii) 615 ÷ 610
(iii) a3 × a2
(iv) 7x × 72
(v) (52)3 ÷ 53
(vi) 25 × 55
(vii) a4 × b4
(viii) (34)3
(ix) (220 ÷ 215) × 23
(x) 8t ÷ 82
Solution:
(i) 32 × 34 × 38 = 32+4+8 = 314 [am ÷ an = am+n]
(ii) 615 ÷ 610 = 615-10 = 65 [am ÷ an = am-n]
(iii) a3 × a2 = a3+2 = a5 [am × an = am+n]
(iv) 7x × 72 = 7x+2 [am × an = am+n]
(v) (52)3 ÷ 53 = 52×3 ÷ 53 = 56 ÷ 53 = 56-3 = 53 [(a3)n = amn, am ÷ an = am-n]
(vi) 25 × 55 = (2 × 5)5 = 105 [am × bm = (ab)m]
(vii) a4 × b4 = (ab)4 [am × bm = (ab)4]
(ix) (220 ÷ 215) × 23 = 220-15 × 23
=25 × 23 = 25+3 = 28
(x) 8t ÷ 82 = 8t-2 [am ÷ an = am-n]
Ex 13.2 Class 7 Maths Question 2.
Simplify and express each of the following in exponential form: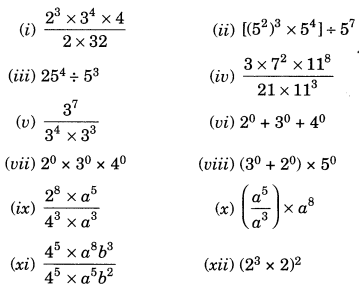
Solution: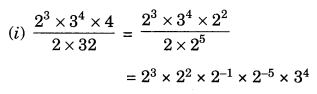
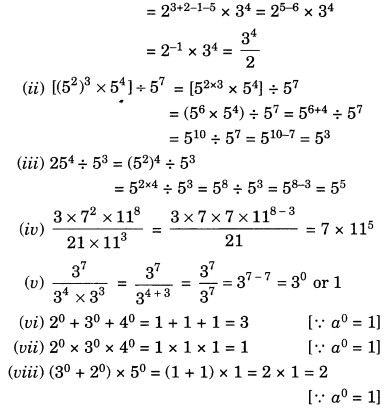
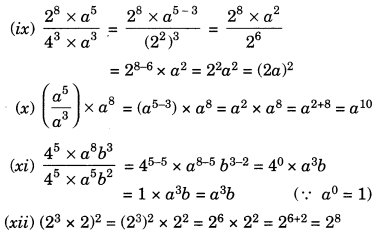
Ex 13.2 Class 7 Maths Question 3.
Say true or false and justify your answer:
(i) 10 × 1011 = 10011
(ii) 23 > 52
(iii) 23 × 32 = 65
(iv) 320 = (1000)0
Solution:
(i) 10 × 1011 = 101+11 = 1012
RHS = 10011 = (102)11 = 1022
1012 ≠ 1022
∴ Statement is false.
(ii) 23 > 52
LHS = 23 = 8
RHS = 522 = 25
8 < 25
∴ 23 < 52
Thus, the statement is false.
(iii) 23 × 32 = 65
LHS = 233 × 32 = 8 × 9 = 72
RHS = 65 = 6 × 6 × 6 × 6 × 6 = 7776
∴ 72 ≠ 7776
∴ The statement is false.
(iv) 30 = (1000)0
⇒ 1 = 1 True [∵ a0 = 1]
Ex 13.2 Class 7 Maths Question 4.
Express each of the following as a product of prime factors only in exponential form:
(i) 108 × 192
(ii) 270
(iii) 729 × 64
(iv) 768
Solution:
(i) 108 × 192 = 2 × 2 × 3 × 3 × 3 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3
=28 × 34
(iii) 729 × 64 = 3 × 3 × 3 × 3 × 3 × 3 × 2 × 2 × 2 × 2 × 2 × 2
=36 × 26
Ex 13.2 Class 7 Maths Question 5.
Simplify: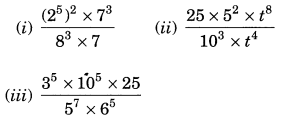
Solution: