अध्याय - 7
सहसंबंध
सहसंबंध
यह एक सांख्यिकीय पद्धति या एक सांख्यिकीय तकनीक है जो विभिन्न चरों के बीच मात्रात्मक संबंध को मापती है, जैसे कीमत और मांग के बीच।
क्रॉक्सटन और काउडेन के अनुसार, "जब संबंध मात्रात्मक प्रकृति का होता है, तो संबंध को खोजने और मापने और इसे एक संक्षिप्त सूत्र में व्यक्त करने के लिए उपयुक्त सांख्यिकीय उपकरण को सहसंबंध के रूप में जाना जाता है।"
सहसंबंध के प्रकार
सहसंबंध को आमतौर पर नकारात्मक और सकारात्मक सहसंबंध में वर्गीकृत किया जाता है।
- सकारात्मक सहसंबंध जब दो चर एक ही दिशा में चलते हैं, तो ऐसे संबंध को सकारात्मक सहसंबंध कहा जाता है, उदाहरण के लिए, कीमत और आपूर्ति के बीच संबंध
- ऋणात्मक सहसंबंध जब दो चर अलग-अलग दिशाओं में बदलते हैं, तो इसे ऋणात्मक सहसंबंध कहा जाता है। कीमत और मांग के बीच संबंध।
सहसंबंध की डिग्री सहसंबंध की
डिग्री सहसंबंध के गुणांक को संदर्भित करती है

(ii) सहसंबंध की अनुपस्थिति
(iii) सहसंबंध की सीमित डिग्री
0 और 1 के बीच सहसंबंध की डिग्री के रूप में मूल्यांकन किया जा सकता है
- उच्च (0.75 और 1)
- मध्यम (0.25 और 0.75)
- कम (0 और 0.25)
सहसम्बन्ध का अनुमान लगाने की विधियाँ
(i) तितर बितर रेखाचित्र बिखरा हुआ आरेख सहसंबंध की दिशा और मात्रा का ग्राफिक व्यंजक प्रस्तुत करता है।
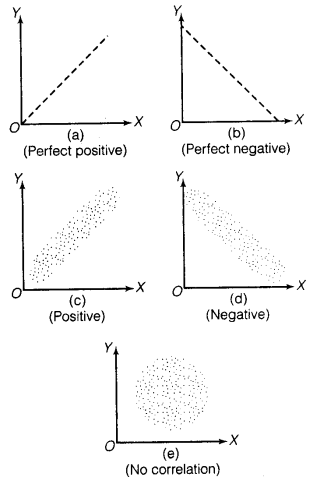
कार्ल पियर्सन का सहसंबंध गुणांक
इसे उत्पाद क्षण सहसंबंध और सरल सहसंबंध गुणांक के रूप में भी जाना जाता है।
कार्ल पियर्सन ने सहसंबंध की गणना की एक मात्रात्मक विधि दी है कार्ल पियर्सन के गुणांक सहसंबंध को आम तौर पर वी के रूप में लिखा जाता है।
फॉर्मूला कार्ल पियर्सन की विधि के अनुसार, सहसंबंध के गुणांक को मापा जाता है
आर =
एक्स वाई _
एन
मैं
एक्समैं
तथा
Where,
r = Coefficient of correlation;
x = x –x¯¯¯
y= y –y¯¯¯
σx = Standard deviation of x series
σy = Standard deviation of y series
N= Number of observations
r = Coefficient of correlation;
x = x –
y= y –
σx = Standard deviation of x series
σy = Standard deviation of y series
N= Number of observations
यदि निम्नलिखित सूत्र का उपयोग करके सीधे x और y के मानक विचलन की गणना करने की कोई आवश्यकता नहीं है
आर =
एक्स वाई _
मैं
एक्स2× _
तथा
2मैंHere, x(x –
शॉर्ट-कट विधि
इस पद्धति का उपयोग तब किया जाता है जब माध्य मान पूर्ण संख्या में नहीं बल्कि भिन्नों में होता है। इस पद्धति में, विचलन की गणना कल्पित माध्य दोनों श्रृंखलाओं को लेकर की जाती है।
सहसंबंध के गुणांक की गणना निम्नलिखित सूत्र का उपयोग करके की जाती है
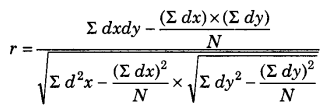
Here, dx = deviation of x series from the assumed mean = (x – A)
dy = deviation of y series from the assumed mean = (y – A)
Σ dxdy – sum of the multiple of dx and dy
Σ dx2 = sum of square of dx
Σ dy2 = sum of square of dy
Σdx= sum of deviation of x-series
Σdy = sum of deviation of y-series
N = Total number of items
dy = deviation of y series from the assumed mean = (y – A)
Σ dxdy – sum of the multiple of dx and dy
Σ dx2 = sum of square of dx
Σ dy2 = sum of square of dy
Σdx= sum of deviation of x-series
Σdy = sum of deviation of y-series
N = Total number of items
चरण विचलन विधि
सहसंबंध के गुणांक की गणना निम्न सूत्र का उपयोग करके की जाती है:
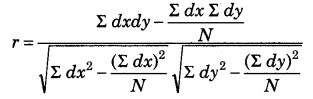
स्पीयरमैन का रैंक सहसंबंध गुणांक
1904 में, 'चार्ल्स एडवर्ड्स स्पीयरमैन' ने गुणात्मक चर के गुणांक सहसंबंध की गणना करने के लिए एक सूत्र विकसित किया। इसे लोकप्रिय रूप से स्पीयरमैन रैंक के रूप में जाना जाता है। अंतर सूत्र या विधि।
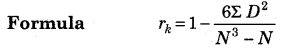
रैंक सहसंबंध का गुणांक जब रैंक समान सूत्र होते हैं
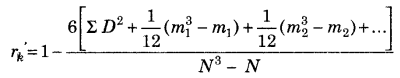
, m = समान रैंक की वस्तुओं की संख्या।
सहसंबंध का महत्व या महत्व
- सहसंबंध का अध्ययन चरों के बीच संबंध की दिशा और डिग्री को दर्शाता है।
- सहसंबंध गुणांक कभी-कभी कारण और प्रभाव संबंध का सुझाव देता है।
- सहसंबंध विश्लेषण व्यावसायिक निर्णयों को सुगम बनाता है क्योंकि एक चर का प्रवृत्ति पथ दूसरे में अपेक्षित परिवर्तनों का सुझाव दे सकता है।
- सहसंबंध विश्लेषण भी नीति निर्माण में मदद करता है।










