Class 11 Economics Chapter 6 परिक्षेपण के माप (Measures of Dispersion) Notes In Hindi

Class 11 Economics Chapter 6 परिक्षेपण के माप (Measures of Dispersion) Notes In Hindi

ECONOMICS 11TH
Published on By Amresh Academy

अध्याय - 6

परिक्षेपण के माप


 फैलाव

"यह वस्तु की भिन्नता का माप है"। स्पीगल के अनुसार, 'संख्यात्मक आँकड़ों का औसत मान के बारे में जिस अंश तक प्रसार होता है, उसे आँकड़ों का विचरण या परिक्षेपण कहते हैं।
परिक्षेपण मापने की विभिन्न विधियाँ हैं

  • श्रेणी
  • चतुर्थक विचलन
  • औसत झुकाव
  • मानक विचलन

R = H – L or L – S
H or L = Highest or Largest value of series
L or S = Lowest or Smallest value of series

Coefficient of range = H−LH+L or L−SL+S

Calculation of Range and Coefficient of Range

(i) व्यक्तिगत श्रृंखला और असतत श्रृंखला

Range = H – L or L – S
Coefficient of Range = H−LH+L or L−SL+S
एच- एलएच+ ली
 या 
एल - एस
एल + एस

(ii) बारंबारता वितरण श्रृंखला

  • वर्ग अंतराल के मध्य मान पाए जाते हैं, उच्चतम और निम्नतम मानों के बीच का अंतर परास होगा।
  • इस पद्धति के अनुसार, हम पाते हैं कि प्रथम वर्ग अंतराल की निचली सीमा और श्रृंखला में अंतिम वर्ग अंतराल की ऊपरी सीमा के बीच का अंतर होगा।

(iii) इंटर क्वार्टाइल रेंज

तीसरे क्वार्टाइल (Q 3 ) और सीरीज के पहले क्वार्टाइल के बीच अंतर को इंटर क्वार्टाइल रेंज कहा जाता है।
IQR = Q3 – Q1

चतुर्थक विचलन
चतुर्थक विचलन अंतर-चतुर्थक श्रेणी का आधा होता है।

QD = Q3−Q12
क्यू3
-
क्यू1
2

इसे सेमी-इंटर क्वार्टाइल रेंज भी कहा जाता है।

(i) चतुर्थक विचलन का गुणांक (QD का

Coefficient of QD = Q3−Q1Q3+Q1
क्यू3
-
क्यू1
क्यू3
+
क्यू1

(ii) चतुर्थक विचलन की गणना

(ए) व्यक्तिगत श्रृंखला और असतत श्रृंखला पहले निम्नलिखित समीकरणों से Q1 और Q 3
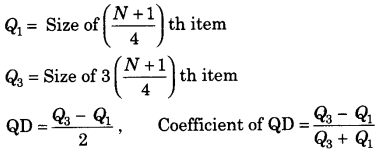
अर्थशास्त्र के लिए सांख्यिकी कक्षा 11 नोट्स अध्याय 6 फैलाव के उपाय 1
का पता लगाएं (बी) आवृत्ति वितरण
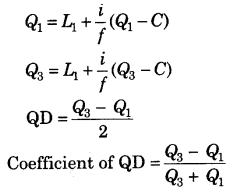
अर्थशास्त्र के लिए सांख्यिकी कक्षा 11 के नोट्स अध्याय 6 विक्षेपण के माप 5

माध्य विचलन
"माध्य विचलन श्रृंखला के सांख्यिकीय औसत से लिए गए सभी मानों के विचलन का अंकगणितीय औसत है। मानों के विचलन को लेते समय, बीजीय चिह्नों + और - को ध्यान में नहीं रखा जाता है, अर्थात् ऋणात्मक विचलनों को भी धनात्मक विचलन माना जाता है।

(i) माध्य विचलन के लिए सूत्र

(a) यदि माध्यिका से विचलन लिया जाता है, तो निम्न सूत्र का उपयोग किया जाता है
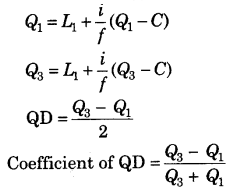
अर्थशास्त्र के लिए सांख्यिकी कक्षा 11 के नोट्स अध्याय 6 परिक्षेपण के माप 4
(b) यदि विचलन श्रृंखला के अंकगणितीय माध्य से लिया जाता है

अर्थशास्त्र के लिए सांख्यिकी कक्षा 11 के नोट्स अध्याय 6 फैलाव के माप 3

(ii) माध्य विचलन का गुणांक

  • Coefficient of mean deviation from Mean = MDX¯¯¯X¯¯¯¯¯
  • Coefficient of MD from Median = MDMM
  • Coefficient of MD from Mode = MDZZ

(iii) माध्य विचलन या माध्य विचलन के गुणांक की गणना 

(a) Individual Series

Estimating MD through Median, MD = Σ|dM|N
Estimating MD through Mean, MD = Σ|dX¯¯¯¯¯|N
Estimating Coefficient of MD through Median Coefficient of MD = MDMM
Estimating Coefficient of MD through Mean Coefficient of MD = MDX¯¯¯X¯¯¯¯¯
एमडी
एक्स
मैंमैंमैं
एक्स
मैंमैंमैंमैंमैं

(b) Discrete Series


Estimating MD through median, MDM = Σf|dm|N
Estimating MD through mean, MDX¯¯¯¯¯ = Σf|dX¯¯¯¯¯|N
Estimating Coefficient of MD through Median Coefficient of MD = MDMN
Estimating Coefficient of MD through Median Coefficient of MD = MDX¯¯¯X¯¯¯¯¯

(c) Frequency Distribution Series


Mean deviation from Median, MDM = Σf|dM|Σf
Coefficient of MD = MDMM
Mean deviation from Mean, MDX¯¯¯¯¯ = Σf|dX¯¯¯¯¯|Σf
Coefficient of MD = MDX¯¯¯X¯¯¯¯¯

एम
डी
एक्स
मैंमैंमैं
एक्स
मैंमैंमैंमैंमैं

मानक विचलन
मानक विचलन वस्तुओं के माध्य मानों से विचलन के वर्गों के अंकगणितीय माध्य का वर्गमूल होता है।

मानक विचलन का गुणांक
यह श्रृंखला के फैलाव का एक सापेक्ष माप है।

Coefficient of standard deviation (Coefficient of σ) = σX¯¯¯¯¯

(i) Calculation of Standard Deviation


(a) Direct Method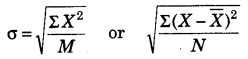
Statistics for Economics Class 11 Notes Chapter 6 Measures of Dispersion 6
Here, σ = Standard Deviation;
ΣX2 = Sum total of the squares of deviation,
X¯¯¯¯ = Mean Value,
X−X¯¯¯¯ = Deviation from mean value;
N = number of items


(b) Short-cut Method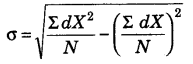
Statistics for Economics Class 11 Notes Chapter 6 Measures of Dispersion 7
(c) Step Deviation Method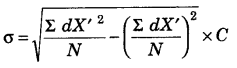
Statistics for Economics Class 11 Notes Chapter 6 Measures of Dispersion 8

(ii) Calculation of Coefficient of Variation
(a) Individual series = σX × 100
(b) Discrete series = σX × 100
(c) Frequency distribution series = σX × 100

लोरेंज वक्र
यह एक ऐसा वक्र है जो वास्तविक वितरण के विचलन को समान वितरण दिखाने से दर्शाता है।
(i) लोरेंज वक्र का निर्माण

  • कक्षा मध्य-बिंदुओं की गणना करें
  • कॉलम 6 . के अनुसार संचयी आवृत्तियों की गणना करें
  • कॉलम 3 और 6 के कुल योग को 100 के रूप में व्यक्त करें और इन स्तंभों में संचयी योग को प्रतिशत में बदलें।
  • अब, ग्राफ पेपर पर, Y-अक्ष पर चर का संचयी प्रतिशत और X-अक्ष का संचयी प्रतिशत लें।
  • निर्देशांक (0, 0) को (100,100) से मिलाने वाली रेखा खींचिए, यह समान बंटन की रेखा कहलाती है।
  • आवृत्ति के संचयी प्रतिशत के साथ चर के संचयी प्रतिशत को प्लॉट करें।
Label :
Amresh Academy

0 comments:

Subscribe to: Post Comments (Atom)