अध्याय - 5
केंद्रीय प्रवृत्ति की माप
केंद्रीय प्रवृत्ति
एक केंद्रीय प्रवृत्ति एक केंद्रीय मूल्य या एक सांख्यिकीय श्रृंखला के प्रतिनिधि मूल्य को संदर्भित करती है।
क्लार्क के अनुसार, "औसत वह आंकड़ा है जो पूरे समूह का प्रतिनिधित्व करता है"।
सांख्यिकीय औसत के प्रकार
औसत को मोटे तौर पर दो श्रेणियों में वर्गीकृत किया जाता है
- गणितीय औसत
- स्थितीय औसत
अंकगणितीय माध्य
अंकगणितीय माध्य वह संख्या है जो एक श्रृंखला के सभी मदों के मूल्यों को जोड़कर और कुल को मदों की संख्या से विभाजित करके प्राप्त की जाती है।
अंकगणित माध्य को सामान्यतः X के रूप में लिखा जाता है। इसे निम्न सूत्र के रूप में व्यक्त किया जा सकता है:
X¯¯¯¯=x1+x2+x3+……xNN or ΣX¯¯¯¯¯N
अंकगणित माध्य के प्रकार
- सरल अंकगणित माध्य
- भारित अंकगणित माध्य
सरल अंकगणित माध्य की गणना के तरीके
(i) व्यक्तिगत श्रृंखला व्यक्तिगत श्रृंखला के मामले में, अंकगणितीय माध्य की गणना दो विधियों द्वारा की जा सकती है
- प्रत्यक्ष विधि इस विधि के अनुसार, हम निम्न सूत्र से अंकगणित माध्य ज्ञात करते हैं:
¯¯¯¯=ΣXN or X¯¯¯¯= Total value of the item Number of items ¯¯¯¯=ΣXN or X¯¯¯¯= Total value of the item Number of items
- शॉर्ट-कट विधि शॉर्ट कट विधि द्वारा, हम निम्नलिखित सूत्र से अंकगणितीय माध्य ज्ञात करते हैं:यहां,
एक्समैंमैंमैंमैं = अंकगणित माध्य, ए = एड का अनुमानित औसत = अनुमानित औसत से विभिन्न मूल्यों के विचलन का शुद्ध योग; और N = श्रृंखला में मदों की संख्या,
(ii) असतत श्रृंखला असतत श्रृंखला के माध्य की गणना करने के तीन तरीके हैं
- प्रत्यक्ष विधि असतत आवृत्ति श्रृंखला के माध्य के आकलन की प्रत्यक्ष विधि सूत्र का उपयोग करती है
एक्समैंमैंमैंमैं=f _एक्सf _ - लघु-कट विधि असतत आवृत्ति श्रृंखला के माध्य का अनुमान लगाने की लघु कट विधि निम्नलिखित सूत्र का उपयोग करती है:
एक्समैंमैंमैंमैं= ए +f _डीf _ - चरण-विचलन विधि यह विधि शॉर्ट-कट विधि का एक प्रकार है। इसे तब अपनाया जाता है जब कल्पित माध्य से विचलन में कुछ सामान्य कारक होते हैं
एक्समैंमैंमैंमैं= ए +f _डीf _× सी
(iii) बारंबारता बंटन आवृत्ति वितरण
में माध्य की गणना करने की तीन विधियाँ हैं
(a) प्रत्यक्ष विधि असतत आवृत्ति श्रृंखला के माध्य के आकलन की प्रत्यक्ष विधि सूत्र का उपयोग करती है
मी = मध्य-मान, मध्य-मान =
एल 1
= वर्ग एल की निचली सीमा 2 = वर्ग की ऊपरी सीमा
(बी) शॉर्ट-कट विधि बारंबारता वितरण के माध्य का अनुमान लगाने की शॉर्ट कट विधि सूत्र का उपयोग करती है
(सी) चरण विचलन विधि इस विधि के अनुसार, हम निम्नलिखित सूत्र द्वारा अंकगणितीय माध्य ज्ञात करते हैं:
(डी) भारित अंकगणितीय माध्य यह श्रृंखला की भारित वस्तुओं का माध्य है। विभिन्न वस्तुओं को उनके सापेक्ष महत्व के आधार पर अलग-अलग भार दिया जाता है। वस्तुओं के भारित योग को भार के योग से विभाजित किया जाता है।
भारित माध्य की गणना
इस प्रकार से, हम निम्नलिखित जानकारी से भारित माध्य ज्ञात करते हैं:
(i) गुण
- सादगी
- यक़ीन
- सभी मदों के आधार पर
- बीजीय उपचार
- स्थिरता
- तुलना का आधार
- शुद्धता परीक्षण
(ii) अवगुण
- अत्यधिक मूल्य का प्रभाव
- माध्य मान श्रृंखला में बिल्कुल भी नहीं आ सकता है
- हास्यास्पद निष्कर्ष
- अनुपयुक्तता
- भ्रामक निष्कर्ष
माध्यिका
"माध्यिका चर का वह मान है जो समूह को दो बराबर भागों में विभाजित करता है, एक भाग में माध्यिका मान से अधिक सभी मान होते हैं और दूसरे भाग में माध्यिका मान से छोटे सभी मान होते हैं"।
(i) माध्यिका की गणना
(a) अलग-अलग श्रृंखला में माध्यिका की व्यक्तिगत श्रृंखला की गणना में निम्नलिखित सूत्र शामिल होता है
M = का आकार
जब श्रृंखला का एन एक सम संख्या है, तो निम्न सूत्र का उपयोग करके माध्यिका का अनुमान लगाया जाता है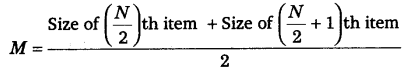
(बी) असतत श्रृंखला या आवृत्ति सरणी के मामले में माध्यिका की असतत श्रृंखला गणना में निम्नलिखित सूत्र शामिल होता है
M = का आकार
(सी) आवृत्ति वितरण श्रृंखला
माध्यिका मान निर्धारित करने के लिए निम्न सूत्र लागू किया जाता है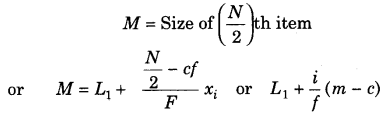
चतुर्थक
यदि एक सांख्यिकीय श्रृंखला को चार बराबर भागों में विभाजित किया जाता है, तो प्रत्येक भाग का अंतिम मान चतुर्थक कहलाता है।
(i) चतुर्थक की गणना चतुर्थक मान (Q 1 और Q 3 ) श्रृंखला के विभिन्न सेटों के लिए अलग-अलग अनुमानित हैं,
(a) व्यक्तिगत और असतत श्रृंखला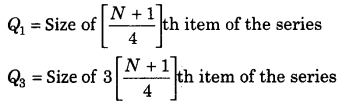
(b) बारंबारता वितरण श्रृंखला आवृत्ति वितरण श्रृंखला में, Q 1 और Q का वर्ग अंतराल 3 को सबसे पहले निम्न के रूप में पहचाना जाता है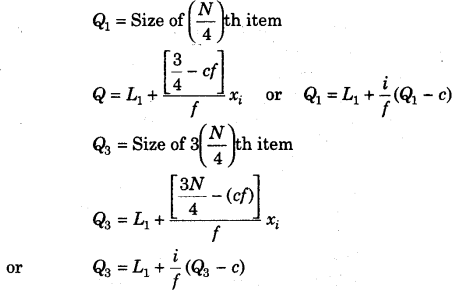
पर्सेंटाइल
पर्सेंटाइल श्रृंखला को 100 बराबर भागों में विभाजित करते हैं, और आम तौर पर पी के रूप में व्यक्त किया जाता है।
विभिन्न प्रकार की श्रृंखलाओं के लिए प्रतिशत का अनुमान लगाया जाता है
(i) व्यक्तिगत और असतत श्रृंखला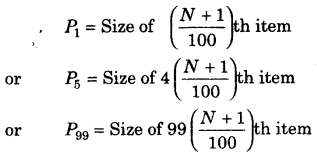
(ii) आवृत्ति वितरण श्रृंखला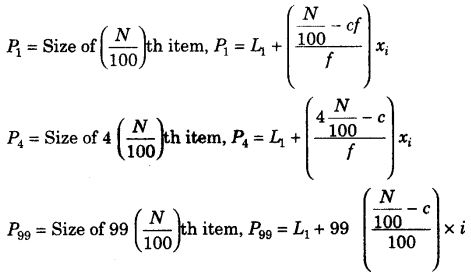
मोड
चर का वह मान जो वितरण में सबसे अधिक बार आता है बहुलक कहलाता है।
क्रॉक्सटन और काउडेन के अनुसार, "मोड को मूल्य की एक श्रृंखला का सबसे विशिष्ट माना जा सकता है"।
(i) मोड की गणना
- व्यक्तिगत श्रृंखला व्यक्तिगत श्रृंखला में बहुलक की गणना के दो तरीके हैं
- निरीक्षण द्वारा
- व्यक्तिगत श्रृंखला को असतत श्रृंखला में परिवर्तित करके
- असतत श्रृंखला मोड असतत आवृत्ति श्रृंखला की गणना के लिए दो तरीके हैं
- निरीक्षण विधि
- समूहीकरण विधि
- आवृत्ति वितरण श्रृंखला बहुलक के सटीक मान की गणना निम्न सूत्र से की जा सकती है:
साथ=ली1+एफ1-एफ02एफ1-एफ0-एफ2एक्समैं
अंकगणित माध्य, माध्यिका और बहुलक की सापेक्ष स्थिति मान लीजिए कि हम व्यक्त करते हैं,
अंकगणित माध्य = M e
माध्य = M i
बहुलक = M o
तीनों का सापेक्ष परिमाण M e > M i > M o या M e < M i < M o है। माध्यिका सदैव अंकगणित माध्य और बहुलक के बीच होती है।










